Student Projects

VE/VM450

Fault Diagnosis Algorithms for Subway Train Doors

Sponsor: Xing Wang, AIMS
Team Members: Yujun Qin, Yinyue Wu, Zhiheng Yin, Qiyue Sun, Yijiao Qin
Instructor: Prof. Shouhang Bo

Project Video

Team Members

Team Members:

Yujun Qin
Yinyue Wu
Zhiheng Yin
Qiyue Sun
Yijiao Qin

Instructor:

Prof. Shouhang Bo

Project Description

Problem

The failure of subway train door takes up to 30% of all the problems in underground transportation. Consequences of door failure are severe. Abnormal opening and closing of train doors can lead to congestion during rush hours, or even hurt passengers. The major failures of induction motors, which is the core component controlling the door, can be broadly classified as bearing related, stator related, rotor related and others, of which bearing related problems take up to 50% [1]. Therefore, building a diagnosis model for subway train door failure is urgent and valuable.

Concept Generation

Raw data collected by sensors include noise which conceal useful signals. Thus, denoising will facilitate the fault diagnosis process. Next, signal transform is performed to amplify the denoised signal. The result transformed signals will be fed to fault diagnosis model. Our solution is decomposed into three sub-problems: Signal Denoise, Signal Transform, and Fault Diagnosis.

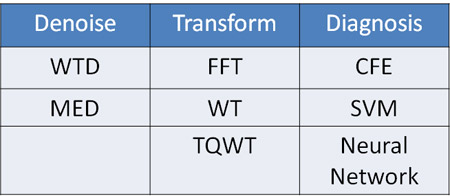
Design Description

– Signal Decomposition: Signal decomposition is a process of separating the components from a composite signal, where w is high-resonance component and c is low-resonance component.

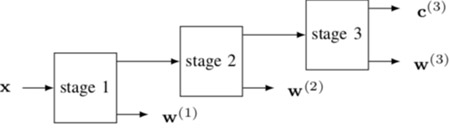
Fig.3 Signal Decomposition

– Signal Denoising: Wavelet-thresholding denoising is an efficient method which sets a threshold value, based on which the larger data remain still or shrink proportionally and the lower ones are cut off to zero. The advantage is to make the pulses easier for analysis.

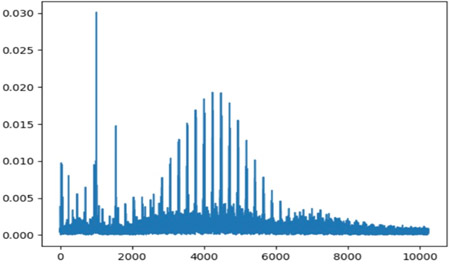
Fig.4 Wavelet Threshold Denoise

– Fault Diagnosis: Hilbert envelope spectrum is used to expose the character frequencies to the low-frequency region. Then we will traverse all the frequencies and compare them to the neighboring frequencies to find the peaks on the spectrum. We pick out those that are at least t times larger than the average of w neighbors.

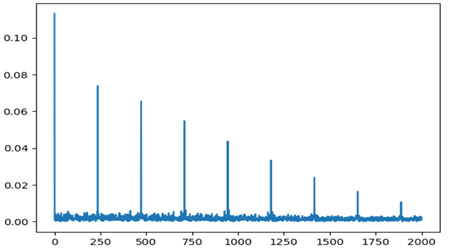
Fig.5 Hilbert Envelop Spectru

Validation

We tested the algorithm on 9464 one-second-signal testcases provided by the sponsor AIMS, which is the all test-cases that we can access.

The expectations are:
– Bearing faults should be detected no later than 30 minutes ahead of the failure
– The algorithm should be able to classify bearing faults as
– outer ring fault
– inner ring fault
– rolling part fault
– no fault
– The precision of the algorithm should be over 70% on the test data, and the recall rate should be over 90% to reduce missed bearing faults
– The complexity of our algorithm should be O(nlog(n)) to ensure time-efficiency

Conclusion

This algorithm is valid and could efficiently solve the realistic problem on subway door problems. This project is on the right track and we are steadily approaching the final stage ofwork.

Acknowledgement

Sponsor:
Xing WANG from AIMS

Reference

[1] W. He, et al., Automatic fault feature extraction of mechanical anomaly on induction motor bearing using ensemble super-wavelet transform, Mech. Syst Signal Process. (2014), http://dx.doi.org/10.1016/j/ymssp.2014.09.007